Master Time and Space Complexity: Optimize Your Algorithms Effectively

Why Understanding Algorithm is More critical Than Ever

In today’s tech-driven world, mastering Data Structures and Algorithms (DSA) has become a fundamental skill for any aspiring software developer or engineer. Whether you’re preparing for coding interviews, competitive programming, or solving real-world problems, DSA forms the backbone of efficient and scalable solutions. In fact, the ability to understand and analyze the algorithm you write is often more critical than just solving a problem. Why? Because it’s not just about finding a solution — it’s about finding the most optimal one.

As companies handle growing volumes of data, the efficiency of algorithms in terms of time and space complexity is crucial. That’s why optimizing code performance is often more important than just solving the problem.

So This Could Be the Right One to Know Everything

What is Time Complexity?

Time complexity is a way to describe how the runtime of an algorithm increases as the input size grows. In simple terms, it tells us how much time an algorithm takes to run depending on the amount of data we give it.

Analogy: Think of it like ordering at a fast-food restaurant. If there’s only one person ahead of you, you’ll get your food quickly. But if there’s a long line of 50 people, it will take much longer to get your food. The length of the line represents the size of the input, and the time it takes to get your order is the time complexity. This illustrates the concept of time complexity: as the input (number of people) grows, the time required for the algorithm here:(order) typically increases as will.

Common Misconceptions About Time Complexity

While time complexity is a powerful tool for analyzing algorithms, there are several misconceptions that beginners often have:

1. “If it works, it’s good enough”: Many new developers assume that if their code produces the correct output, it’s a good solution. However, correctness alone isn’t sufficient. For example, a brute-force solution might work for small inputs but become impractically slow for large datasets.
2. “Fast code is always better”: Just because an algorithm runs quickly for small inputs doesn’t mean it will scale well. For instance, an O(n²) algorithm might seem fast when n is 10, but when n grows to 1,000, the runtime could skyrocket.
3. “Time taken by the code execution is the same as time complexity”: Many beginners mistakenly believe that the actual time taken for code execution directly reflects its time complexity. However, this is not the case. Various factors, such as CPU speed and system architecture, can affect execution time, making it distinct from the theoretical measure of time complexity.

Understanding time complexity and recognizing common misconceptions are essential for developing efficient algorithms. By grasping these concepts, developers can create solutions that not only work correctly but also perform well under varying input sizes.

Steps to Compute Time Complexity

When computing time complexity, especially as a beginner, there are three key principles to follow:

1. Always Consider the Worst-Case Scenario: Worst case refers to the situation where the algorithm performs the maximum number of steps. This is crucial because it gives you the upper bound of how long an algorithm could take, even in the most challenging cases.

• For example, if you’re searching for an element in a list, the worst case is when the element is at the very end (or not found at all), requiring the algorithm to check every single item.
• Why worst case? It ensures we’re prepared for the most time-consuming situation, which is essential for evaluating efficiency.

2. Avoid ConstantsAvoiding constants: means we focus on how the algorithm scales with large inputs rather than small fixed values. Constants (like +1, +2, or multiplying by a small number) don’t significantly impact performance when input size becomes large.

• Example: Consider an algorithm that takes 2n + 3 steps. While “2” and “3” are constants, they matter very little when n becomes extremely large, so we simplify the complexity to just O(n).
• Relating it to the analogy: If you’re waiting in line with 50 people, whether you’re delayed by 2 or 3 extra seconds doesn’t matter much — it’s the total number of people (input size) that determines how long you’ll wait.

3. Avoid Lower ValuesWhen computing time complexity, we focus on large input sizes, as that’s when the efficiency of an algorithm really matters. Small inputs might not reveal the true scaling behavior of your code.

• For example, an algorithm with complexity O(n²) might seem fast for small inputs like n = 5, but as n grows (e.g., to 1,000), the difference between O(n) and O(n²) becomes dramatic.
• Relating it to the analogy: If only 3 people are ahead of you, the time complexity might not seem like a concern. But when there are 50 or 100 people in line, the way the algorithm handles larger inputs is what makes a real difference.

Step 2 helps you simplify time complexity by ignoring small constants in the expression.

Step 3 encourages you to analyze the algorithm’s performance with large input sizes rather than focusing on small, trivial cases.

Best, Average, and Worst Case in Algorithms

When analyzing algorithms, we consider three possible scenarios for performance and three notations:

Big O, omega, theta

1. Best Case (Ω Notation): This is when an algorithm performs its fastest. For example, in a linear search, if the target element is the first in the list, the search ends in constant time, which is Ω(1).
2. Average Case (Θ Notation): This is the expected performance, typically when inputs are random. For instance, finding an element in the middle of a list takes around half the time, making it Θ(n/2), but simplified to Θ(n).
3. Worst Case (O Notation): This scenario assumes the most time-consuming input, like searching for the last element or not finding it at all. This makes the time complexity O(n) in linear search.

Why Do We Use Big O? Worst-Case Guarantees: Big O ensures that no matter the input, the algorithm won’t perform worse than expected.

Scalability: Focusing on worst-case scenarios helps ensure that your algorithm can handle large and unpredictable datasets effectively.

Practicality: While average and best-case scenarios (Θ and Ω) are useful, they aren’t always reliable in real-world applications, where ensuring worst-case performance is crucial.

Types of Time Complexities

Time complexity helps us understand how the runtime of an algorithm grows with input size. The most common types of time complexities, in order of their efficiency from best to worst, are:

1. Constant Time – O(1)
2. Logarithmic Time – O(log n)
3. Linear Time – O(n)
4. Linearithmic Time – O(n log n)
5. Quadratic Time – O(n²)
6. Exponential Time – O(2ⁿ)

1. Constant Time – O(1)

• Definition: The runtime of the algorithm does not change with the size of the input. It always takes the same amount of time, no matter how large or small the input is.
• Example: Accessing an element in an array by its index.

int getFirstElement(int arr[], int n){

  //Always takes the constant time to access the first element.

  return arr[0];  
}

No matter how large the array is, accessing the first element always takes constant time.

2. Logarithmic Time – O(log n)

• Definition: Logarithmic time complexity occurs when an algorithm’s runtime increases much more slowly than the input size. This typically happens when the algorithm repeatedly divides the input size in half to find a solution.
• Mathematical Insight: For an input size of n, binary search completes in log₂(n) steps. Searching through 16 elements takes 4 steps, and for 1,000 elements, it takes around 10 steps, which is significantly faster than linear search.

why is it called Logarithmic?

The number of operations grows logarithmically because the problem space is reduced exponentially with each step. For example, binary search splits the search space in half at every step.

Real-World Analogy

Imagine finding a word in a dictionary. Instead of checking every word one by one, you flip to the middle, decide if the word is before or after, and then repeat by halving the search space. This is why binary search operates in O(log n) time — a far more efficient approach for large datasets.

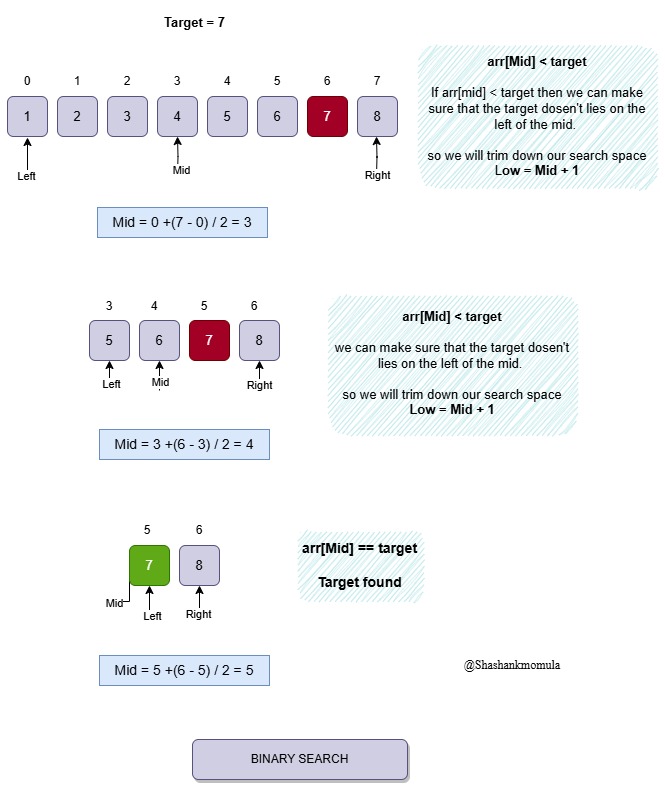
Eample: Binary Search Algorithm

Target : 7

int binarySearch(int arr[], int n, int target){
  int left = 0, right = n-1; //O(1)

while(left<=right){  
// O(log n): The loops run logarithmically based on the size of input
    int mid = left+(right-left)/2;   //O(1)

    if(arr[mid] == target) return mid;
    else if(arr[mid] < target) left = mid+1;
    else right = mid-1;
}
return -1;  //O(1)
}

3. Linear Time – O(n)

• Definition: Linear time complexity, denoted O(n), means that the runtime grows directly in proportion to the input size. if the input doubles, the time it takes to complete the task also doubles.

Example: Linear Search Algorithm

A linear search algorithm is a classic example of this. It checks each element in an array one by one until it finds the target value.

int linearSearch(int arr[], int n, int target){

for(int i=0; i<n; i++){ //O(n) Iterating through all elements
    if(arr[i] == target){ // O(1) checking the current element
      return i;
    }
  }
return -1; //O(1) if target is not found
}

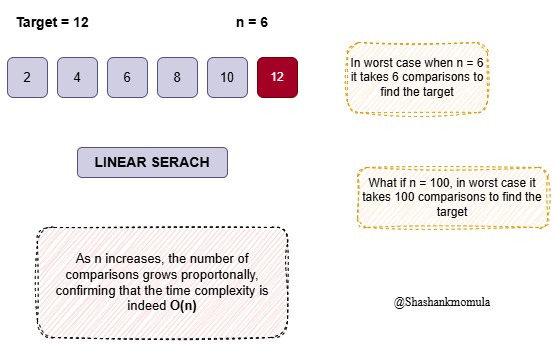
Why is it O(n)?

In the worst case, the algorithm checks all n elements before finding the target or concluding it’s not present. Thus, the number of operations increases linearly with the input size.

Real-World Analogy:

Imagine searching for a book in a library, checking each book one by one. If there are 100 books, you might check all 100; if there are 1,000 books, it could take up to 1,000 checks. This reflects the linear growth of time with the input size.

4. Linearithmic Time – O(n log n)

• Definition: Linearithmic time complexity, denoted as O(n log n), means the runtime grows in proportion to n times the logarithm of n. This complexity often shows up in efficient algorithms that involve both dividing a problem and processing each part. You may wonder: why n, why log n, and how do these combine? Let’s explore with a real-world analogy for better understanding.

Real-World Analogy for O(n log n) – Sorting Jumbled ID Cards of a Class

Imagine you have 50 jumbled ID cards, and your task is to arrange them in order by student number. Sorting all 50 cards at once would be overwhelming, so you decide to use a divide-and-conquer approach, similar to how merge sort works.

Dividing the ID Cards – O(log n):

First, you repeatedly divide the cards into smaller groups. Split 50 cards into two piles of 25, then split those again, and so on until you have single cards.

Each time you halve the pile, you’re reducing the problem size, taking log n steps. For example:

50 cards → 25 cards → 12 cards → 6 → 3 → 1.

This step takes O(log n) because you’re dividing the cards in half until you can’t divide anymore.

Sorting and Merging – O(n):

Now that each card is a single pile, you start merging.

At each step, you compare and combine two piles of cards in the correct order. To merge two piles, you need to touch each card once, making this step O(n), where n is the total number of cards.

Why Does This Process Take O(n log n)?

O(log n) comes from the repeated division of the cards into smaller groups.

O(n) comes from the merging process, where you sort and combine each card back together.

In short, you’re dividing the problem into smaller pieces in log n steps, and for each division, you’re sorting all the cards, making the overall complexity O(n log n).

Now let’s look at how this works in an actual algorithm with the merge sort code:

void mergeSort(int arr[], int l, int r){

  if(l<r){
    int m = l+(r-l)/2; // Find the middle
    mergeSort(arr,l,m); // Sort the first half
    mergeSort(arr,m+1,r); // Sort the second half
    merge(arr,l,m,r); // Merge the sorted halves
 }
}

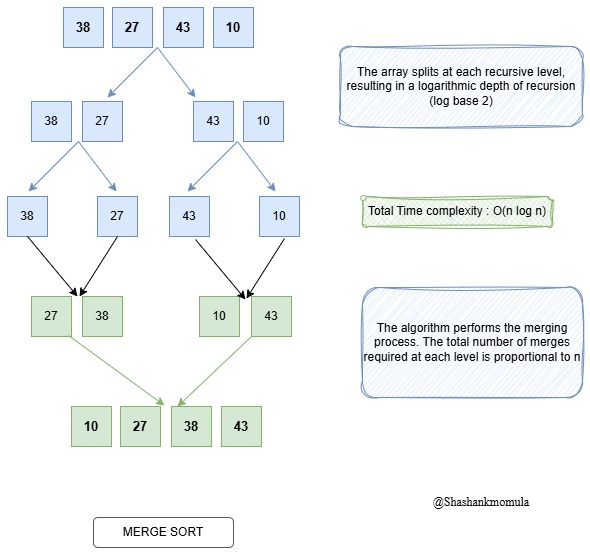
When you first look at the merge sort code, you might wonder, What is mergeSort()? What is merge()? Don’t worry! It’s just a sorting algorithm that breaks the array into smaller parts, sorts them, and then merges them back together.

To fully understand how this works, take a moment to explore it for yourself. Here’s a simple breakdown:

• mergeSort() is the function that splits the array into smaller parts until each part is a single element.
• merge() is the function that combines those single elements (or smaller arrays) back together in sorted order.

Once you start diving deeper into it, you’ll find merge sort to be an elegant and efficient way of sorting!

Give it a try, and you’ll see it’s not as scary as it looks!

5. Quadratic Time – O(n^2)

• Definition: Quadratic time complexity, denoted as O(n^2), means that the runtime grows in proportion to the square of the input size. This is common in algorithms where each element needs to be compared or processed with every other element, often leading to nested loops.

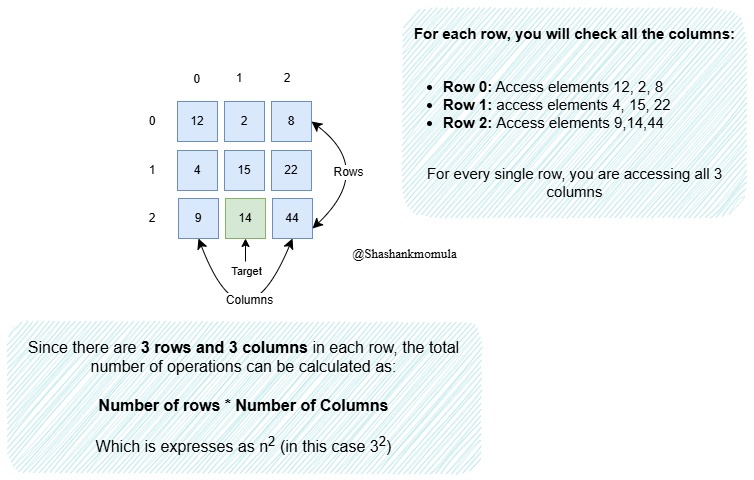
Example: Accessing Elements in an n×n Matrix(2D)

Imagine you have an n×n grid (like a matrix), and you need to perform some operation on each cell in the grid or you need to find a target element, one by one. Since there are n rows and n columns, this results in n×n = n^2 operations in total, as every element in each row is accessed once per column.

bool findElement(int matrix[3][3], int target){
  for(int i=0;i<3;i++){ //outer loops iterates over rows
    for(int j=0;j<3;j++){ //inner loop iterates over columns
      if(matrix[i][j] == target){
        return true;
      }
    }
  return false;
}

6. Exponential Time Complexity – O(2^n)

Exponential time complexity, denoted as O(2^n), describes an algorithm where the runtime doubles with each additional input element. This complexity is among the slowest and quickly becomes unfeasible for even moderately large inputs, often appearing in recursive algorithms that branch into multiple subproblems — such as the naive recursive solution to the Fibonacci sequence.

Example: Calculating the Fibonacci Sequence (Recursive Approach)

In the Fibonacci sequence, each number is the sum of the previous two. A simple recursive approach to calculate this follows:

int fibonacci(int n){
  if(n<=1)return n;
  return fibonacci(n-1)+fibonacci(n-2);
}

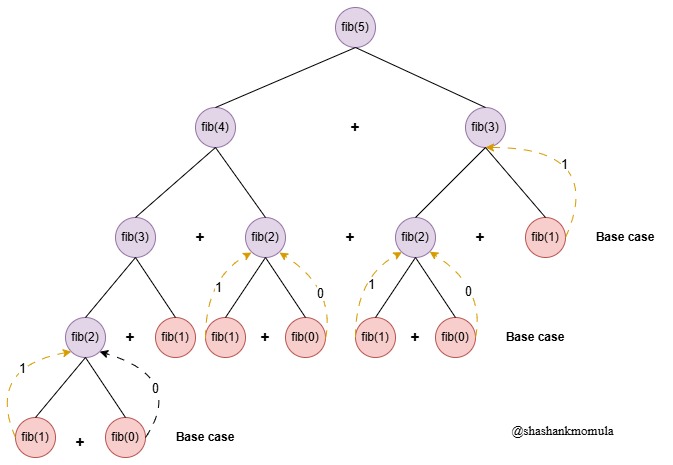
In this code, each call to fibonacci(n) branches into two further calls for fibonacci(n-1) and fibonacci(n-2), resulting in a branching factor of 2. For an input size of n, the total number of recursive calls grows roughly as 2^n.

Why Exponential?

Each recursive call leads to two more, making the process double with every increase in input size. For example, calculating fibonacci(5) is manageable, but fibonacci(40) would require over a billion calls due to the exponential growth.

Real-World Analogy: Folding a Piece of Paper

Imagine folding a piece of paper in half. The thickness doubles with each fold: 2 layers on the 1st fold, 4 on the 2nd, 8 on the 3rd, and so on. After 20 folds, the paper would have over a million layers! Similarly, exponential algorithms quickly become impractical, as their growth doubles with every additional input. Just as you can only fold a paper so many times, exponential algorithms rapidly become unmanageable with even small increases in input size.

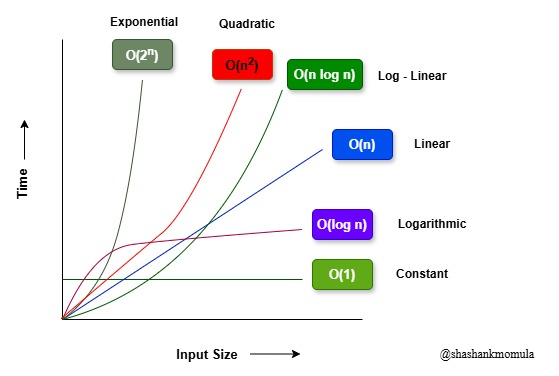
1. O(1) – Constant Time: The time remains constant regardless of the input size, making it the fastest and most efficient time complexity. Examples include accessing an element by index in an array.
2. O(log n) – Logarithmic Time: As the input size increases, the time grows very slowly. This is often seen in algorithms that repeatedly halve the input, like binary search.
3. O(n) – Linear Time: The time complexity grows linearly with the input size. For example, a single loop iterating over n elements takes O(n) time.
4. O(n^2) – Quadratic Time: The time complexity grows quadratically, often seen in algorithms with nested loops. Sorting algorithms like bubble sort have this complexity.
5. O(2^n) – Exponential Time: The time grows extremely fast as n increases, making it impractical for large inputs. Recursive algorithms that solve all subsets, such as solving the traveling salesman problem, have this complexity.

From this comparison, O(1) and O(log n) are the most efficient, while O(n^2) and O(2^n) should generally be avoided for large inputs due to their steep growth rate. Choosing the right algorithm with a lower time complexity significantly impacts performance, especially as the input size grows.

What is Space complexity?

Space complexity measures the extra memory an algorithm needs to run efficiently, calculated as a function of the input size. It helps us estimate how much storage an algorithm will use by analyzing the memory needed for components like variables, data structures, function calls, and temporary storage.

Components of Space Complexity

Fixed Memory Requirements:

• Constants: Fixed values like configuration settings that do not change with input size.
• Primitive Variables: Basic counters or indexes, which remain constant regardless of input.

Variable Memory Requirements:

• Data Structures: Memory for structures like arrays or lists, which grow with the input.
• Function Call Stack: For recursive algorithms, each call adds to the stack until all calls are resolved.
• Temporary Storage: Memory for intermediate results, such as buffers or temporary arrays.

Real-World Analogy: Packing a Suitcase

Imagine packing a suitcase:

• Essentials vs. Extras: Essentials (core memory) are always needed, while extras represent additional memory for optional tasks.
• Efficient Packing: Like minimal packing, using only necessary memory keeps the algorithm efficient.
• Limited Capacity: Just as a suitcase has limited space, computers have finite memory; using memory efficiently is crucial.

Example: Reversing an Array

To reverse an array, a naive approach is to create a new array to store elements in reverse order, which requires extra memory proportional to the input size, giving an O(n) space complexity. For large inputs, this approach could be inefficient due to increased memory usage.

In summary, space complexity is essential for understanding and minimizing the memory requirements of an algorithm, particularly in environments where memory is limited.

1. O(1) – Constant Space Complexity: The algorithm uses a fixed amount of memory regardless of the input size. Examples include algorithms that only use a few variables, like swapping two numbers.
2. O(n) – Linear Space Complexity: The memory usage grows linearly with the input size. For example, storing n elements in an array or a list requires O(n) space.
3. O(n²) – Quadratic Space Complexity: The space required increases quadratically with the input size, such as a 2D array of size n x n. This type of complexity can quickly become inefficient as input size grows.

Conclusion

Optimizing both time and space complexity is crucial for building efficient algorithms. By understanding and selecting the right time and space complexity, you can make your algorithms faster and more memory-efficient, leading to smoother, more scalable applications.

Optimizing your code is like sharpening a tool — the sharper it is, the better it performs. Aim for efficiency, and let your algorithms do more with less.